I postulati di Euclide

Gli Elementi di Euclide costituiscono il primo vero e proprio trattato di geometria razionale che ci sia pervenuta.

Le varie nozioni geometriche vengono sistematicamente organizzate dal greco Euclide in una teoria assiomatica che le collega tra di loro mediante ragionamenti deduttivi.

Euclide suddivide questi principi in postulati e nozioni comuni (assiomi).

La distinzione tra postulato e assioma è piuttosto sottile.

Elenchiamo i postulati che incontriamo nel libro di Euclide:

1. da qualsiasi punto si può condurre una retta a ogni altro punto.
2. ogni tratto di retta può essere prolungato indefinitamente.
3. con ogni centro e ogni distanza si può descrivere un cerchio.
4. tutti gli angoli retti sono uguali tra loro.
5. per ogni punto del piano si può condurre una retta e una soltanto, parallela a una retta data, non passante per il punto.

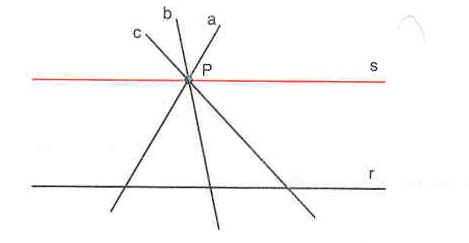
Per il punto P passano infinite rette complanari alla r;
il loro insieme è detto fascio di rette di sostegno P.
Tra queste rette ve ne è una ed una sola, dice il 5° postulato, che non interseca la r.
Nel disegno questa retta, la sola parallela alla r per P, è rappresentata dalla retta s.

INDICE