Poligoni inscritti e circoscritti

Se si disegna un triangolo ABC si può vedere che per i 3 vertici si può disegnare un'unica circonferenza: in questo caso si dice che il poligono è inscritto nella circonferenza e che questa è circoscritta al poligono.

Questo vale per qualsiasi poligono i cui vertici sono punti di una circonferenza.

Si chiama circocentro il centro della circonferenza circoscritta al triangolo ed è il punto di incontro degli assi dei lati del triangolo.

L’incentro è un altro punto con caratteristiche di equidistanza dai 3 lati: è il punto comune delle bisettrici del triangolo ed è equidistante dai 3 lati.

Le proiezioni sui 3 lati formano una circonferenza inscritta nel triangolo.

Il raggio della circonferenza circoscritta al poligono si chiama raggio del poligono, il raggio della circonferenza inscritta si chiama apotema.

In ogni poligono inscritto in una circonferenza, l’area è minore del cerchio G ma è sempre più prossima a quella della circonferenza all’aumentare dei lati del poligono.

Poligoni inscritti ad una circonferenza

In ogni poligono circoscritto l’area è sempre maggiore di quella del cerchio G , ma essa si avvicina a quella del cerchio all’aumentare dei lati del poligono.

Partendo da queste affermazioni, Archimede intuì che l’area del cerchio è l’elemento di separazione tra l’insieme dei poligoni inscritti e quello dei poligoni circoscritti. Se facessimo aumentare all’infinito il numero dei lati avremmo la perfetta coincidenza fra poligono inscritto, cerchio e poligono circoscritto.

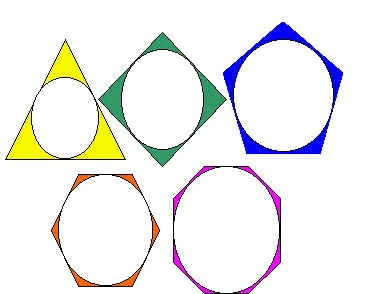
Poligoni circoscritti ad una circonferenza

INDICE